29-反转链表II

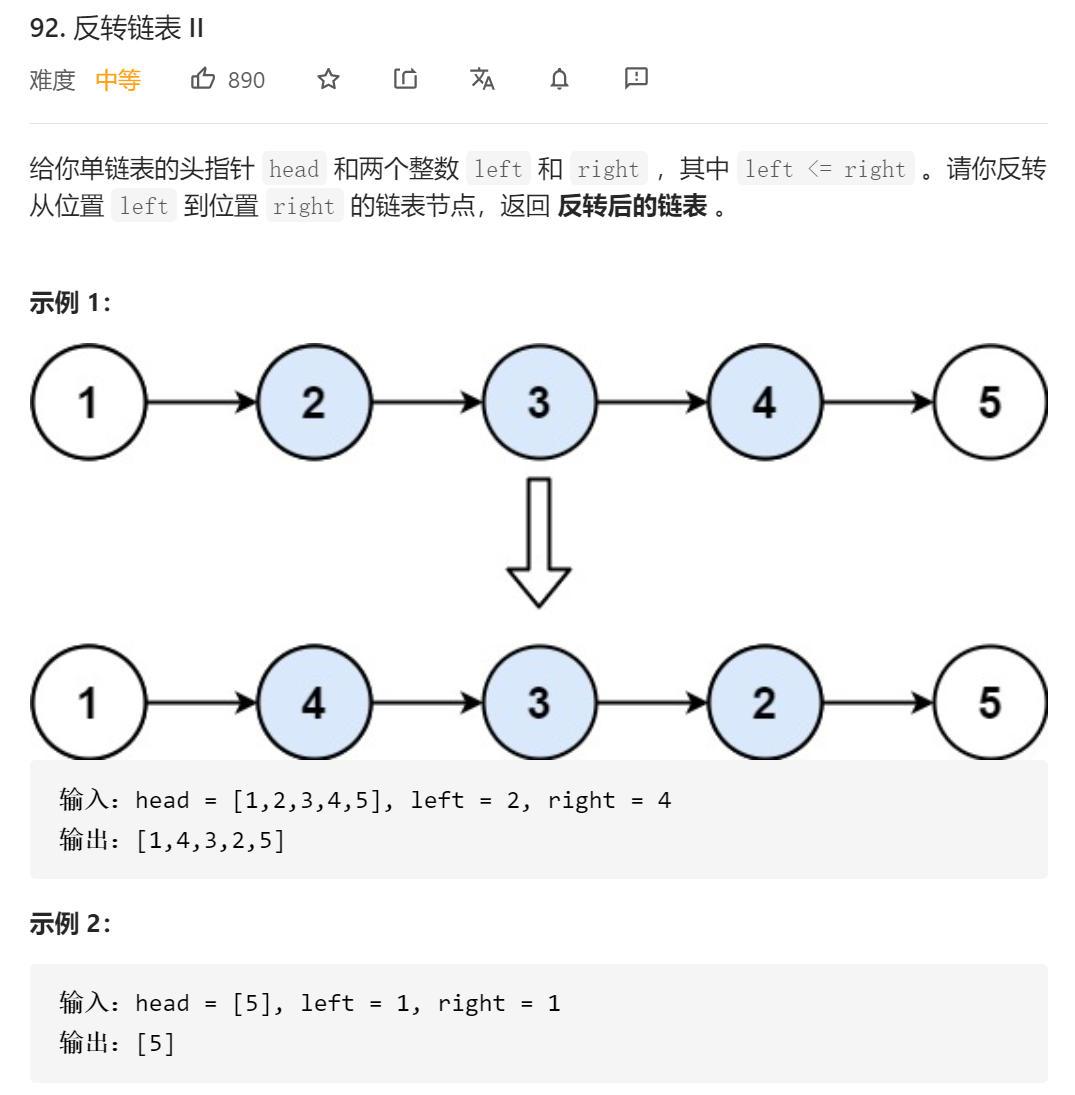
自己的做法

算法思想

反转部分链表，那就找到该链表的头节点，并将尾节点的next置为null，变成一个独立的链表，然后使用反转链表题目中的算法。

此时，还剩前一段链表和后一段链表，分别使用两个指针来指针前一段链表的尾节点和后一段链表的头节点，用于链表反转后的拼接。

同时注意，因为链表头节点头可能会被反转，所以添加一个哑节点。

算法思想

class Solution {
public:
    void reverse(ListNode * head) {
        ListNode * pre = nullptr;
        ListNode * cur = head;
        while (cur) {
            ListNode * temp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = temp;
        }
    }
    
    ListNode * reverseBetween(ListNode* head, int left, int right) {
        ListNode * dummy = new ListNode();
        dummy->next = head;
        //前一段链表的尾节点
        ListNode * pre = dummy;
        for(int i = 0; i < left - 1; i++) {
            pre = pre->next;
        }
        ListNode * start = head;
        ListNode * end = head;
        for(int i = 0; i < left -1; i++) {
            start = start->next;
        }
        for(int i = 0; i < right -1; i++) {
            end = end->next;
        }
        //后一段链表的头节点
        ListNode * rear = end->next;
        end->next = nullptr;

        reverse(start);

        pre->next = end;
        start->next = rear;

        return dummy->next;
    }
};

性能分析

时间复杂度：$O(n)$。

空间复杂度：$O(1)$。

参考做法

参考给了两种做法，第一种叫穿针引线，其实就是我那种做法。

第二种做法给出了第一种做法的优化。

因为第一种做法，虽然时间复杂度是$$O(n)$$，但是当left和right差距很大时，实际是遍历了链表两次，找到待反转头尾节点试一次，进行反转又是一次。

第二种做法优化了一下。

算法思想

同样还是分前一段链表和后一段链表。

遍历待反转节点，每访问一个节点，就将该节点放到前一段链表的尾节点的下一个位置处。

使用三个指针：pre，cur，next，他们的意义是：

• pre永远指向待反转链表的前一个节点，即前一段链表的尾节点
• cur指向待反转节点，即用来遍历待反转链表
• next指向cur节点的下一个节点

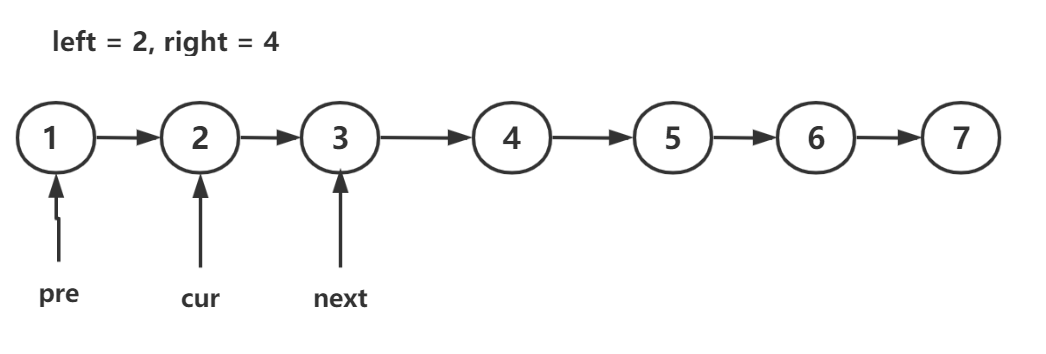
然后按下面步骤来做：

1. cur的下一个节点指向next的下一个节点，以图为例就是，节点2指向节点4
2. next的下一个节点指向pre的下一个节点，以图为例：节点3指向节点2
3. pre的下一个节点指向next，即节点1指向节点3

这样就完成了一个节点的反转。

算法实现

class Solution {
public:

    ListNode * reverseBetween(ListNode* head, int left, int right) {
        ListNode * dummy = new ListNode();
        dummy->next = head;
        //前一段链表的尾节点
        ListNode * pre = dummy;
        for(int i = 0; i < left - 1; i++) {
            pre = pre->next;
        }
        ListNode * cur = pre->next;
        ListNode * next;

        for(int i = 0; i < right - left; i++) {
            next = cur->next;
            cur->next = next->next;
            next->next = pre->next;
            pre->next = next;

        }

        return dummy->next;
    }
};

性能分析

时间复杂度：只遍历了一次链表，$O(n)$。

空间复杂度：$O(1)$。