31-环形链表 II

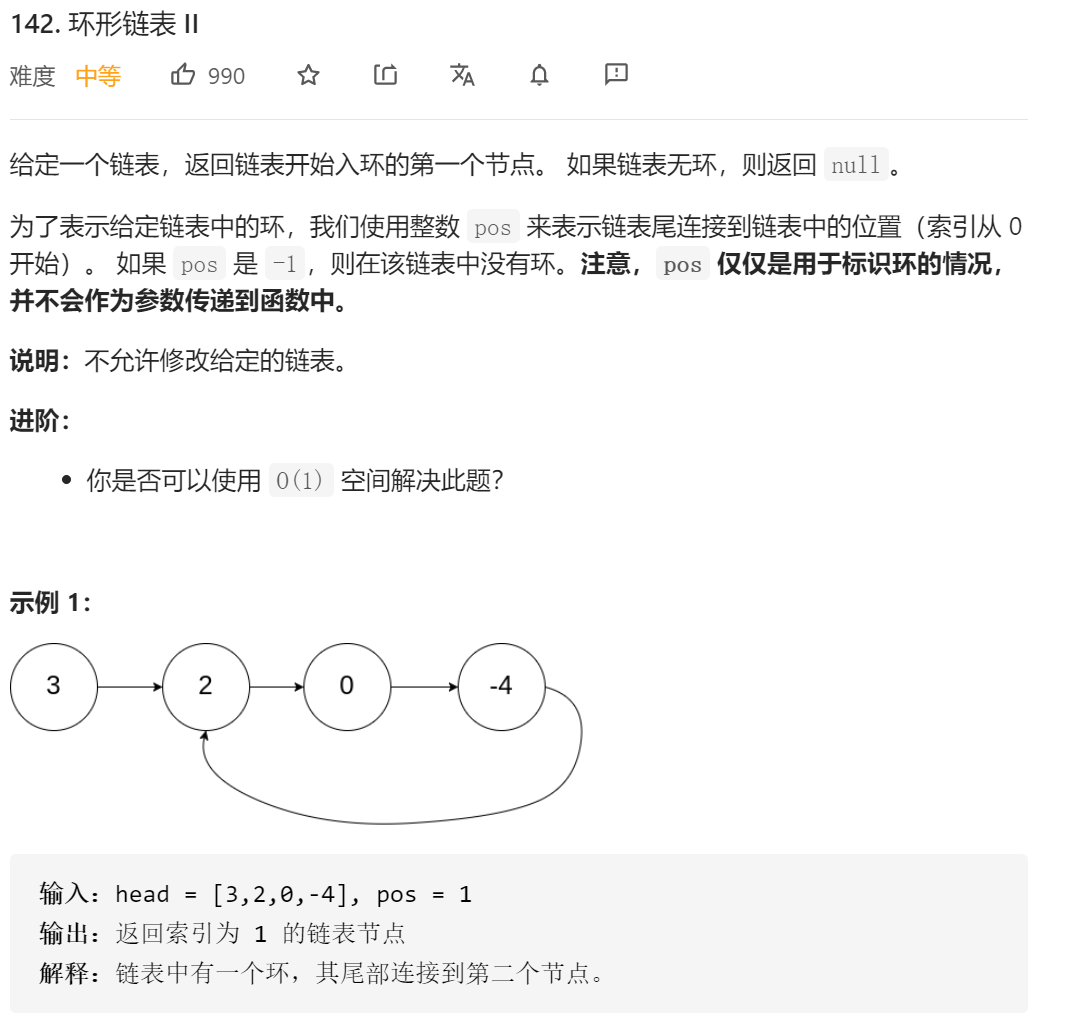
自己的做法

算法思想

哈希表法。

使用已访问集合，即一个set集合来保存已访问过的节点指针。

遍历链表，每访问一个节点，检查它的next节点是否在集合中。

如果不存在，则将它的next节点存到字典中，并访问下一个节点；如果存在则当前节点就是链表尾节点，入环的第一个节点就是当前节点的next节点。

同时，注意判断当前节点的next节点是否为空。

算法实现

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(head == nullptr || head->next == nullptr) {
            return nullptr;
        }
        unordered_set<ListNode *> nodes;
        nodes.insert(head);
        ListNode * cur = head;
        while (cur->next && !nodes.count(cur->next)) {
            nodes.insert(cur->next);
            cur = cur->next;
        }
        return cur->next;

    }
};

性能分析

时间复杂度：遍历链表，$O(n)$。

空间复杂度：使用set集合，$O(n)$。

参考做法

算法思想

快慢指针法。

使用两个指针fast和slow，开始两指针都指向头节点，然后fast每次走两步，slow每次走一步。如果链表有环，则fast指针和slow指针一定会在环内某个节点相遇。

如图，设从链表头节点到入环第一个节点距离为a,入环第一个节点到相遇点距离为b，相遇点走到入环第一个节点距离为c。

那么当两指针相遇时，设fast指针在环中走了n圈。

则fast指针所走的距离为：$$a + n(b +c) + b$$。，又 fast指针走的距离一定是slow走的距离的两倍。

即：$$a + n(b + c) + b = 2(a + b)$$。

化简得：$$a = c + (n - 1)(b + c)$$。即，从相遇点走到入环第一个节点，再走n - 1圈的距离和头节点到入环第一个节点的距离a相等。

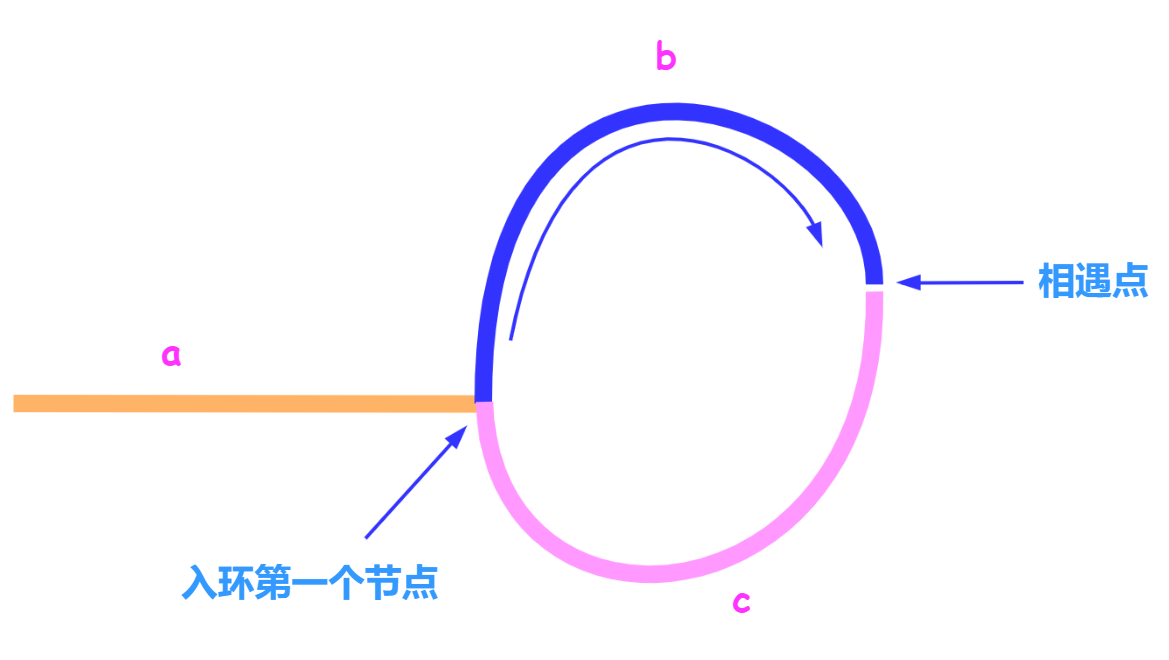
因此，当fast指针和slow指针相遇时，再设一个指针node指向头节点，slow和node指针同时向后走，它们会在入环第一个节点相遇。

算法实现

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode * fast = head;
        ListNode * slow = head;
        while (fast) {
            if(fast->next == nullptr || fast->next->next == nullptr) {
                return nullptr;
            }
            fast = fast->next->next;
            slow = slow->next;

            if(slow == fast) {
                ListNode * node = head;
                while (slow != node) {
                    slow = slow->next;
                    node = node->next;
                }
                return node;
            }
        }
        return nullptr;

    }
};

性能分析

时间复杂度：$O(n)$。

空间复杂度：$O(1)$。