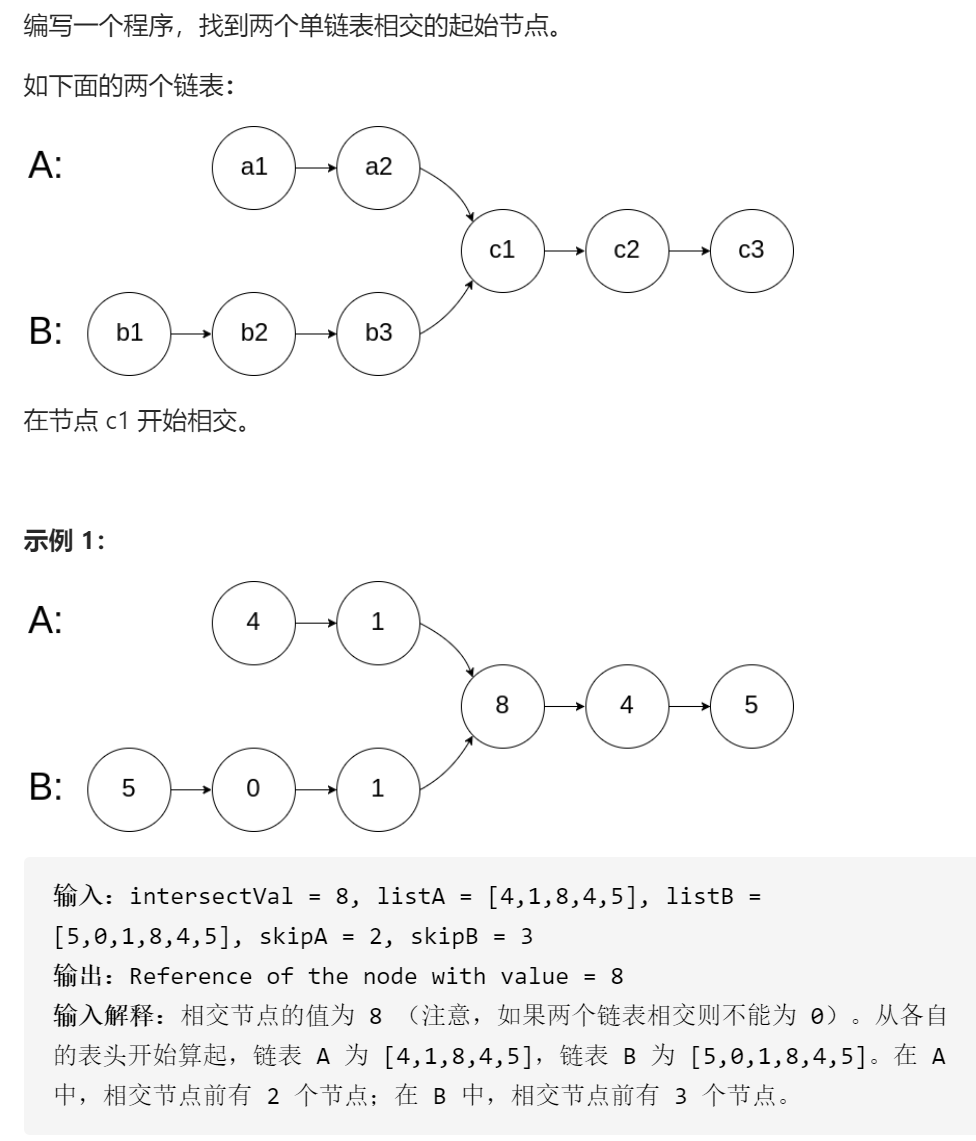
4-相交链表

自己的解法

算法思想

使用哈希表，首先遍历链表B，将每个链表地址存入set集合。然后遍历链表A，对于链表A的每个节点，在set集合中查找有没有地址相同的元素，如果有，则该节点就是第一个交点。

如果遍历到A链表末尾依然没有，那么这两个链表不相交。

算法实现

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};

class Solution {

public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(headA == nullptr || headB == nullptr) {
            return nullptr;
        }
        set<ListNode *> address;
        ListNode * b = headB;
        while (b != nullptr) {
            address.insert(b);
            b = b->next;
        }
        ListNode *a = headA;
        while (a != nullptr) {
            if(address.count(a)) {
                return a;
            }
            a = a->next;
        }
        return nullptr;

    }
};

更好的解法

算法思想

双指针法。这种解法非常巧妙。

我们设链表A的节点数为a，链表B的节点数为b，它们的公共节点数为c。第一个公共节点(就是交点)为node。

定义两个指针pA和pB分别指向链表A和链表B，同时向后遍历，当pA遍历到A链表末尾，就重定向到链表B头结点；

同样的，当pB遍历到B链表结尾，就重定向到链表A头结点。

当指针pA遍历B链表走到node节点时，遍历的节点数是：a + (b - c + 1)，即走了a + b - c步。

当指针pB遍历A链表走到node节点时，遍历的节点数是：b + (a - c + 1)，即走了b + a - c步。

注：这里的加1，就是加上第一个公共节点。

因此指针pA和pB会同时到达公共节点。

• 当c = 0时，即A、B链表没有交点，那么pA和pB最终会指向null。
• 当c > 0时，pA和pB会同时指向交点。

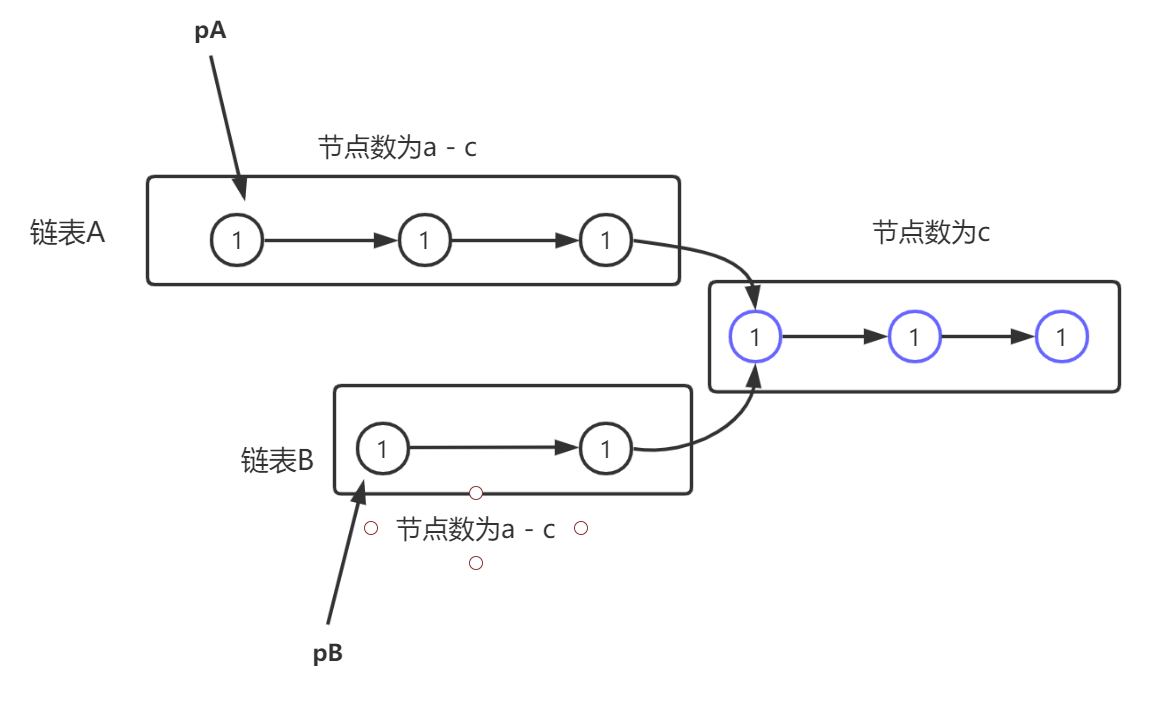
这种方法就是用了A + B = B + A的思想。虽然各自路程不同，但加起来的路程是相等的。速度一样，最终一定会同时到达。

算法实现

class Solution {

public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(headA == nullptr || headB == nullptr) {
            return nullptr;
        }
        ListNode *pA = headA;
        ListNode *pB = headB;
        while (pA != pB) {
            pA = pA!= nullptr ? pA->next : headB;
            pB = pB!= nullptr ? pB->next : headA;
        }
        return pA;
    }
};

性能分析

• 时间复杂度：最差情况是链表没有交点，此时时间复杂度为$O(a + b)$
• 空间复杂度：只用了两个指针，$O(1)$。

贴一个leetcode解法的评论(哈哈哈哈哈哈哈)：

| 这个算法也太浪漫了吧，错的人迟早会走散，而对的人迟早会相逢。